Andrew King – 2015
1. INTRODUCTION
Artificial intelligence and machine learning are rapidly growing fields of research for many companies, universities and research organizations. Many researchers are beginning to utilize one model for machine learning in particular: the artificial neural network. Traditionally, creating a neural network has typically involved hard-coding a fixed topology of the network. More recently, however, researchers have begun experimenting with the use of genetic algorithms in conjunction with neural networks to select the topology.
The most popular topology evolving algorithm is named NEAT: the neuroevolution of augmenting topologies. Neuroevolving neural networks evolve in a manner similar to natural selection. Due to their constantly evolving nature, neuroevolving neural networks have the capacity to increase in efficiency, accuracy and complexity over time to better perform a task. This key difference gives neuroevolution algorithms the potential to create networks beyond the level of complexity that programmers can model manually. In this paper, I will discuss the NEAT neuroevolution algorithm. I will explain the basic principles of its operation as well as the areas in which it excels — in regards to both efficacy and complexity of outcomes — when compared with traditional approaches.
2. BACKGROUND
2.1. Neural Networks
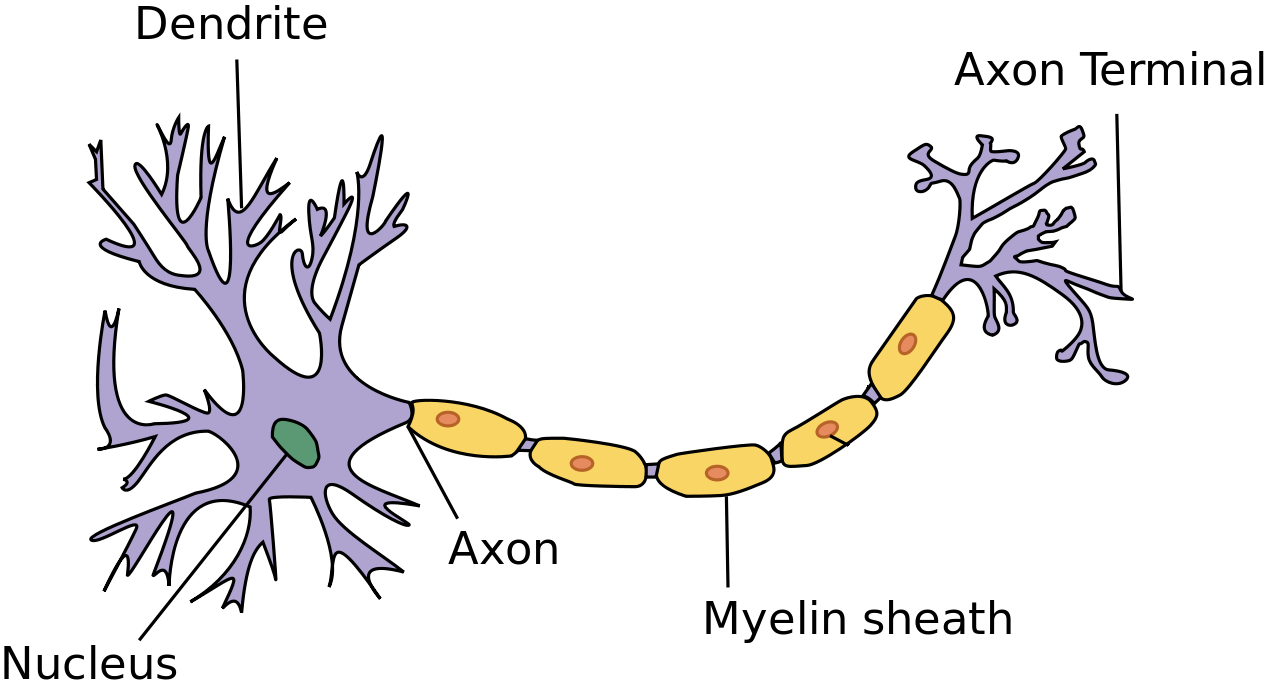
In order to understand the meaning of this paper, it is important to have a working knowledge of artificial neural networks. These neural networks are very roughly inspired by biological neural networks in the human brain. Biological neural networks involve a series of interconnected neurons that transfer electrical impulses. On one side of each neuron there are dendrites that receive inputs. These inputs are directed away from the nucleus into the axon. During this process the inputs are summed. In most cases, neurons only have one output (which can communicate with several other neurons) but they will have many inputs, sometimes up to 100,000 [Roberts 2016]. Artificial neural networks function in much the same way, receiving many inputs (X₁ and X₂ in Fig 1). These inputs carry different weights (w in Fig 1). The inputs are multiplied by their respective weights and then summed to one input (i in Fig 1). They then pass through an activation function (g in Fig 1), which determines the output (y in Fig 1) of the artificial neuron [Heaton 2011]. For the neuron shown in figure 1, the various inputs will produce the following results for the given activation function.
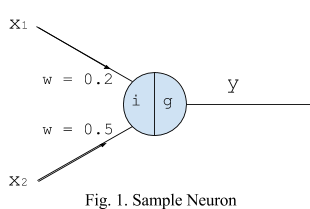


The output for the given neuron with stated weights and activation function produces the logical AND function as seen in figure 2. The activation function essentially pushes the step or curve left or right (example shown in figure 3). The same functionality can be achieved by adding another input to the neuron, in which case the input is referred to as a bias [Luger 2008].Given a different activation function or set of weights, the neuron could produce any linearly separable logical function. In functions where the inputs are not linearly separable (the XOR, for instance) multiple neurons are required. To train a neural network for problems that are not linearly separable, one makes use of backpropagation. Backpropagation is an algorithm that calculates the error of a network’s weights and propagates it backward through the network so that the weights can be adjusted and the network can be trained. Backpropagation is crucial in multilayered neural networks.
There are many practical applications for supervised neural networks. One such application that I worked on as part of my research in neural networks was a music genre classifier. It would take a music file and output a prediction of the genre with about 80% accuracy. For this, I created a standard multilayered neural network that can receive multiple input variables and give a single output: the genre prediction. In my specific implementation, I classified the genre based on only low-level audio features (extracted from the waveform). These factors included such things as spectral centroid average, beat sum, and waveform compactness. The network used a single hidden layer and would output a genre prediction. There are also far more complex uses for neural networks. For example, I worked with a few projects which made use of the University of California, Berkeley’s Caffe Deep Learning Framework for neural networks. One application of Caffe called “Neural Style,” can receive a style image as its input and, after capturing the style in the network, can then apply that style to other images by passing them through the network [Jia 2016]. The weights of the network could be shifted in favor of style over the supplied content image, or vice versa. Additionally, the content image could be passed through the network a set number of times to slowly refine the final output. See the provided figure and Appendix 1 for examples of the images created with this application using the Caffe Deep Learning Framework.
2.2. Neuroevolution
Neuroevolution is a form of reinforcement learning, meaning that incoming data is raw and not marked or labeled. Instead, specific actions are rewarded or discouraged. NEAT makes use of evolutionary algorithms to train neural networks and evolve topologies in an automated fashion [Stanley 2002]. Traditional neural networks have taken the form of supervised learning, where inputs are labeled and the network is trained with a series of these marked inputs. NEAT is as the name suggests: it will evolve as neural networks do, by adjusting the weights of the different inputs, but will also evolve in topology or structure. This means that a relatively simple neural network can evolve to become extremely complex over time to better suit and accomplish a task. This form of learning is called reinforcement learning and it makes use of a fitness function to define its failure or success. NEAT starts by searching the search space of simple networks and then looks at increasingly complex networks. This is called complexification [Stanley 2004].
There are many use cases for neuroevolution. NEAT has been used in many fields, from physics calculations to game development [Miikkulainen 2006]. Researchers at Fermilab used NEAT to compute the most accurate current measurement of the mass of the top quark at the Tevatron Collider. In a paper detailing the quark mass measurement project, the researchers said, “Poor performers are culled and strong performers are bred together and mutated in successive generations until performance reaches a plateau. Because we have optimized directly on the final statistical precision rather than some intermediate or approximate figure of merit, the best-performing network is the one which gives the most precise measurement. This approach has been shown to significantly outperform traditional methods in event selection. In particular, we use neuroevolution of augmenting topologies (NEAT), a neuroevolutionary method capable of evolving a network’s topology in addition to its weights” [Aaltonen, et al. 2009]. As this project shows, NEAT is multifaceted in its application and has potential to outperform the traditional approach to neural networks.
As this project shows, NEAT is multifaceted in its application and has potential to outperform the traditional approach to neural networks.
On the other end of the spectrum, NEAT was used in the MarI/O project written by Seth Bling. Bling created a complex fitness function to measure performance in the game Super Mario World. He created a NEAT neural network that was able to play the game autonomously and it was able to complete the first level of Super Mario World after 33 generations of evolution [Bling 2015].
As part of my research, I studied and evolved a NEAT neural network to predict solar radiation 12 hours in the future given a series of inputs about present conditions. It used 6 inputs such as wind speed, air temperature, current time of day, and rainfall. This implementation began as a single neuron and had to grow in order to increase its accuracy. The fitness function was very simply defined as the mean absolute error, which NEAT would evolve the network to minimize.
There are a number of parameters that can be adjusted and must be specified in any NEAT neural network implementation. The most commonly adjusted are the population size, elitism, maximum fitness threshold, initial setup features and the probability of adding certain topological features. To understand the way NEAT works, it is important to understand the purpose and function of each of these parameters individually. The population size specifies how many individual networks are produced in each generation. Elitism specifies how many individuals survive from one generation to the next. The most fit (as measured by the fitness function) will survive. Maximum fitness threshold specifies a fitness level which will terminate the evolution of the network if it is reached. The initial setup features allow for specification of the desired number of nodes and layers to begin with. Finally, the probability of adding certain topological features, such as new neurons or connections, can be specified.
3. ADVANTAGES OF NEUROEVOLUTION
3.1. No Need for Labeled Training Data
There are many advantageous reasons to implement neural networks using principles from neuroevolution. The most obvious advantage of neuroevolution is the fact that it does not require network training with labelled data (though it can be used this way if desired). This means that NEAT can work in domains where data is currently nonexistent or sparse. This was quantitatively demonstrated by a team of researchers who concluded that, “Empirical evaluations against the performance of state of the art statistical machine learning methods such as support vector machine show that NEAT-evolved ANN classifier outperforms by an average of 9.96% higher accuracy when presented with [a] very small training set proving its superior ability to generalize its learning” [Hasanat, et al. 2008]. Unlike more traditional methods, neuroevolution relies on a fitness function that simply determines how well the network is performing. The potential drawback to this is that in some domains, the fitness functions may be difficult to define, though not impossible.
3.2. The Generic Nature of Neuroevolution
Another defining aspect of neuroevolution is its generic nature. This means that all applications can generally start with a common base, where the only difference is the fitness function. The network can be evolved to complexity, efficacy and efficiency from a simple perceptron [Stanley 2004]. Traditional neural networks can require large amounts of setup and customization to arrive at an optimal topology for a network. Because neuroevolving networks are based on a fitness function, they can quickly adapt to changes in incoming data for maximum accuracy when circumstances change. Biological brains in mammals can be seen as operating in much the same way. Rather than being inherently complex, they are more the product of an evolutionary fitness function. This sentiment was reflected by a receiver of the ACM Turing Award, Herbert A. Simon, who said, “Human beings, viewed as behaving systems, are quite simple. The apparent complexity of our behavior over time is largely a reflection of the complexity of the environment in which we find ourselves” [Simon 1981].
Traditional neural networks, however, would need additional training data to maintain performance. They also need to be regularly fine-tuned based on that data because they are just regulated by the data they are given rather than being checked against performance. Their topologies may also need to be modified to remain accurate as circumstances change. As we have discussed, neuroevolution can adapt to changing circumstances. According to an article on adaptive behavior discussing NEAT, “many domains would benefit from online adaptation . . . learning gives the individual the possibility to react much faster to environmental changes by modifying its behavior during its lifetime. For example, a robot that is physically damaged should be able to adapt to its new circumstances” [Risi and Stanley 2010]. All of these points serve to illustrate the generic nature of neuroevolution in neural networks.
3.3. Unmatchable Complexity and Necessary Abstraction
Another defining feature of NEAT — and neuroevolving neural networks generally — is its ability to create large and complex neural networks. Some problem spaces require very complicated topologies in order to have the desired output. There is no direct way to generate the most efficient topology for a network. NEAT is helpful in this arena because it imposes a genetic algorithm to evolve networked topologies, selecting traits from the most successful networks and eliminating the least successful. Eventually, these topologies and networks can grow beyond the realm of reasonable human investment. Neuroevolving neural networks evolve the topology to be efficacious without the need of a human programmer understanding its complexity. This further illustrates the superiority of utilizing neuroevolution over more traditional methods. Kenneth Stanley, creator of NEAT, echoed this idea in his dissertation on the subject, saying, “Sophisticated behaviors are difficult to discover in part because they are likely to be extremely complex, perhaps requiring the optimization of thousands or even millions of parameters. Searching through such high-dimensional space is intractable even for the most powerful methods…. [NEAT is] a method for discovering complex neural network-controlled behaviors by gradually building up to a solution in an evolutionary process called complexification” [Stanley 2004].
This presents us with the idea that abstraction may be a necessary part of future artificial intelligence. There are some applications where traditional methods of programming would be extremely inefficient and very difficult to become efficacious. For example, neural networks are particularly useful in image recognition programs because of the complexity of the task of accurately recognizing patterns in millions of different images. If these programs were hard-coded, they would take far more time and would be difficult to reach a high level of accuracy.
However, with this complexity and abstraction, one cannot be absolutely certain that unexpected behaviors will not arise. One outlier or anomaly in the data could cause erratic behaviors. The unpredictability of neuroevolution thus both warrants some criticism as well as praise. In some domains where security is paramount, the evolutionary paradigm and complex topologies may give rise to unintended consequences [Pugh and Stanley 2013]. For example, neural networks have been frequently researched for their ability to predict stock prices. This approach has been shown to have the capability to be quite successful, “results indicat[ing] that, despite its simplicity, both in terms of input data and in terms of trading strategy, such an approach to automated trading may yield significant returns” [Azzini, et al. 2008]. If trading organizations were to adopt a neuroevolving neural network to make trades on their behalf, irregularities in the algorithm could make it a riskier investment than hardcoded fixed topology neural networks. It is not unreasonable however, that given some hard coded security measures, neuroevolution could be used in these high-stakes environments.
3.4 Novelty from Randomness
While unexpected behaviors can be viewed as a disadvantage to neuroevolution, it is also potentially one of the greatest advantages of neuroevolution. It is not reasonable to assume that we will always come up with the best behaviors for performance. As long as the fitness function is being met and the network is behaving efficaciously, unintended complex behaviors can be beneficial and even desirable. We cannot always anticipate the best performance behaviors a priori. Therefore, novel behaviors are often exactly the kind of behaviors that we want to occur. In this sense, even the seemingly unexpected is often actually a sought-after benefit of neuroevolution [Risi and Stanley 2010].
4. CONCLUSIONS
In summary, I have covered artificial neural networks, their relation to biological neural networks, and their basic structure and use case. I then described neuroevolution and the specific implementation of NEAT. NEAT and other neuroevolving neural networks have many key attributes that make them useful and efficacious. Neuroevolving neural networks do not require network training and can thus work in domains where data is nonexistent or sparse. Additionally, their generic nature provides them with the advantage of being able to start from a simple, common space and still be able to evolve to complexity, efficacy, and efficiency. Neuroevolution also creates larger, more complex neural networks than most traditional approaches. And finally, the novel aspect of neuroevolution can also be advantageous because we cannot always anticipate the best performance behaviors, making the sometimes unintended, complex behaviors from neuroevolution beneficial and even desirable.
All of these aspects illustrate how neuroevolution poses a new paradigm within artificial intelligence, specifically the realm of neural networks. This paradigm embraces the thought that great things can be accomplished without us even having to labor or understand every detail of their operation. Rather than spending the majority of our time working on implementation, we work on creating the conditions where greatest implementation can give rise to itself.
The algorithms in neuroevolution can theoretically generate immense complexity. Currently, we hardly understand the complex, intelligent processes that we see in nature, and yet we strive to reproduce their function in artificial intelligences. Neuroevolution presents an alternative paradigm, where we simply seek to create the conditions of nature and let the complexity exceed our understanding once again. For this reason, neuroevolution is poised to fully utilize the potential of neural networks as we develop artificial intelligence in the future.
